| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 직관
- 창원nc파크
- 텐동텐야
- 신해바라기 분식
- LG TECH CONFERENCE 2023
- 담화탁주
- 프로야구
- 원정응원단석
- 환상자전거길
- 후기이벤트참여
- network slicing
- 아이오닉5
- sk와이번스
- 전복 김밥
- 롯데시네마 현풍
- 리클라이너석
- 티스토리챌린지
- 제주도
- 원정
- 5G
- 술담화
- 올스타전
- 드림라이브존
- 제주도 자전거여행
- 오블완
- 제주 담스테이
- SK 와이번스
- 일엽편주
- V1구역
- 오스너예가다이얼
- Today
- Total
개루프이득의 블로그
수치적 적분: 적분의 근사 방법 본문
<설명에 사용된 그래프 그림은 아래 링크에서 가져왔습니다.>
http://tutorial.math.lamar.edu/Classes/CalcII/ApproximatingDefIntegrals.aspx
Calculus II - Approximating Definite Integrals
We already know that \(n = 4\), \(a = 0\), and \(b = 2\) so we just need to compute \(K\) (the largest value of the second derivative) and \(M\) (the largest value of the fourth derivative). This means that we’ll need the second and fourth derivative of \(
tutorial.math.lamar.edu
정적분을 처음 배울 때로 돌아가보자.
우리는 정적분을 그래프 아래의 면적으로 정의를 했고, 이를 리만합으로 표현을 하여 구간의 크기를 극소값으로 극한을 보내면서 적분을 정의했었다.
하지만, 우리는 적분을 계산할 때 항상 리만합을 이용해서 구하지는 않는다. 그저 우리가 아는 공식대로, 그리고 터득한 스킬들로 문제를 풀게 된다.
그렇다면 수치적 적분을 배우고 적분의 근사에 대해서 공부하는 이유는 무엇일까?
일단 가장 기본적으로는, 컴퓨터는 생각보다 멍청해서 우리가 푸는 것 처럼 적분을 풀어주지를 못 한다. 컴퓨터에서는 리만합을 구하듯이 수치적으로 극소값들을 모두 더해주면서 적분을 풀어주게 된다. 즉, 적분의 근사 방법을 배우면 적분에 대해서 이해를 하는 것에 도움이 될 뿐만 아니라 컴퓨팅의 관점에서도 조금 친숙해질 수 있을 것 이라고 생각된다. 이번 글에서는 적분의 근사법들을 소개하고 이를 matlab으로 간략하게 구현을 해보는 것 까지 다루려고 한다.
1. Midpoint Approximation
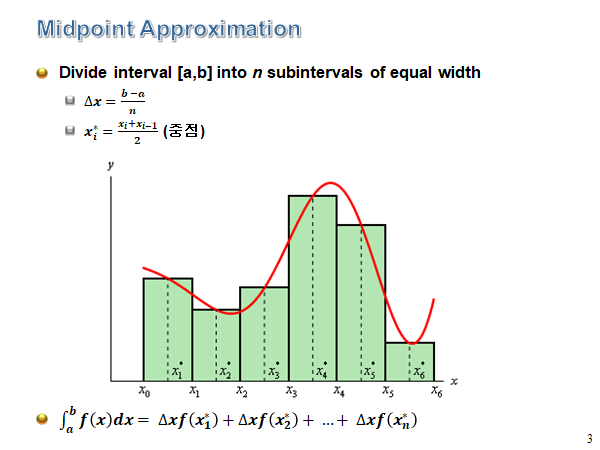
가장 많이 접해본 근사 방법일 것 같다. 적분구간 [a,b]를 n개의 구간으로 나눈다고 할 때, 하나의 작은 직사각형을 중앙값의 함수값으로 근사를 해주어서 구하는 방법이다.
2. Trapezoid Approximation

다음은 사다리꼴 공식이라고 알려진 방법인데, midpoint method와 마찬가지로 구간을 나눠주고, 하나의 단위 넓이를 사다리꼴로 근사를 시켜줘서 구하는 방법이다.
3. Simpson's Approximation


마지막은 simpson's method인데, 여기서의 핵심 아이디어는 구간에서 세점을 기준으로 하여, 점 세개가 주어지면 하나의 유일한 이차함수가 정해지기 때문에, 그 이차함수의 넓이로 근사를 시키겠다는 것이다. 하지만, 직접 매 구간마다 이차함수를 구해주고, 그 적분값을 구해주는 것 역시 꽤 많은 연산량을 요구하게 되는데, 이 적분값이 위의 그림과 같이 각 함수값들의 선형합 꼴로 표현이 된다는 것이 증명되어 이 근사방법 역시 비교적 쉽게 구할 수 있게 되어 많이 사용되는 근사방법 중 하나이다.
4. Matlab 구현
더 많은 근사법들이 있겠지만, 위의 세가지 방법에 대해 matlab으로 직접 구현을 해볼 예정이다. 이 내용을 사실 matlab을 처음 접해보는 사람들을 기준으로 준비를 했기 때문에, 구현은 매우 간단하다.
4-1. Midpoint Approximation
function I = midpoint (f, a, b, n)
h=(b-a)/n;
xi=a:h:b;
I = 0;
for j = 1:1:n
I = I + f(((xi(j)+xi(j+1))/2)) * h;
end
end코드블럭이 matlab은 지원을 안 해서 조금 그렇긴 한데...;; 아무튼, 위와 같이 midpoint method를 간단하게 함수로 구현할 수 있다. 이 함수는 I라는 적분값을 output으로 가지며 input으로는 적분하고자하는 함수 f, 적분 구간 a, b 그리고 구간의 개수 n을 받게 된다.
코드 내용은 뭐 보면 알겠지만, h라고 하나의 구간의 크기를 구해준 다음에, for문을 돌면서 하나하나 구간마다의 크기를 계속 더해줘서 근사값을 구해주는 구조이다.
4-2. Trapezoid Approximation
function I = trapezoid (f, a, b, n)
h=(b-a)/n;
xi=a:h:b;
I = 0;
for j = 1:1:n
I = I + (f(xi(j))+f(xi(j+1))) * h/2;
end
endmidpoint method와 구현은 거의 똑같고, for문 안에 계산해주는 부분만 사다리꼴의 넓이로 수정해서 구해주게 된다.
4-3. simpson's Approximation
function I = simpsons(f,a,b,n)
h=(b-a)/n;
xi=a:h:b;
I= h/3*(f(xi(1))+2*sum(f(xi(3:2:end-2)))+4*sum(f(xi(2:2:end)))+f(xi(end)));
endsimpson의 경우는 적분의 근사값을 구할 때, 계수가 2배, 4배가 되는 부분이 계속 규칙적으로 나온다는 것을 이용해서 for문을 쓰는 대신 sum이라는 명령어를 이용해서 한 줄에 구해줄 수 있도록 구현을 했다.
4-4. 각 근사법들 비교
f = @(x) 1./x;
a = 0.5;
b = 10;
I_mid = 2:2:50;
I_tra = 2:2:50;
I_sim = 2:2:50;
for i = 2:2:50
I_mid(i/2) = midpoint(f, a, b, i);
I_tra(i/2) = trapezoid(f, a, b, i);
I_sim(i/2) = simpsons(f, a, b, i);
end
n = 2:2:50;
plot(n, I_mid)
hold on
plot(n, I_tra)
plot(n, I_sim)
legend('midpoint', 'trapezoid', 'simpsons');마지막으로, 1/x의 그래프에 대해서 [0.5, 10]구간의 적분값으로 수렴하는 모습을 그래프로 비교를 해봤다. 내가 매트랩은 많이 안 쓰기도 하고, 그냥 생각나는대로 해서 발코딩이긴 한데, n이 작을때부터 해서 충분히 커질 때 까지의 근사값들을 모두 저장하여서 그래프로 그려주었다.

그 결과 위의 그래프처럼 각 method 별로 수렴하는 것을 확인할 수 있었다.
<추가된 내용>
이 수업들을 원격으로 해서 내 유튜브 계정에 수업 영상들이 남아있었는데, 혹시나 해서 일부공개는 그대로 넣어놓고 재생목록을 만들어두었으니 도움이 될지는 모르겠지만 관심 있으면 아래에서 영상도 확인할 수 있습니다.
https://youtube.com/playlist?list=PLT8Ck3FhPFERRvX1Y1_Ukq97u6z6pkyCG
'전공 공부' 카테고리의 다른 글
| Laplace Transform Matlab으로 해보기 (0) | 2020.05.12 |
|---|---|
| 행렬의 기초 (0) | 2020.04.21 |
| 다양한 적분 방법 : 삼각치환법과 부분 분수를 이용한 적분 (0) | 2020.03.31 |
| 함수의 극한 정의 : 입실론-델타 논법 (4) | 2020.03.24 |
| Delay jitter란 무엇이고, 왜 필요할까 (2) | 2019.11.14 |




