| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 올스타전
- 5G
- 일엽편주
- SK 와이번스
- 원정
- 원정응원단석
- 담화탁주
- 제주도 자전거여행
- 후기이벤트참여
- 제주 담스테이
- network slicing
- 드림라이브존
- V1구역
- 전복 김밥
- 텐동텐야
- 제주도
- 롯데시네마 현풍
- 오스너예가다이얼
- LG TECH CONFERENCE 2023
- 직관
- 아이오닉5
- 술담화
- 오블완
- 티스토리챌린지
- 신해바라기 분식
- 프로야구
- 창원nc파크
- 환상자전거길
- 리클라이너석
- sk와이번스
- Today
- Total
개루프이득의 블로그
행렬의 기초 본문
대학교 입학했을 때 부터 고등학교 교육과정이 개편이 되면서 행렬에 대한 부분이 모두 교육과정에서 빠진다는 흉흉한 소문을 들었었다. 이번에는 행렬에 대한 기본적인 설명을 하게 되었는데, 고등교육과정에서 어느 정도로 배우는지 알 수 없기 때문에 교육과정이 어떻게 바뀌게 되었는지 고3때 담임선생님이 수학 과목이셨어서 연락을 해서 물어보게 되었다.
개편이 되면서 일반고의 정규교육과정에서는 아예 행렬에 대해서 배우지 않게 되었고, 특목고에서만 심화과목으로 배운다고 한다.
대학수업을 위해 준비를 하는 것이긴 하지만, 1학년 학생 대상으로 하는 수업이고 일반고출신인 입장에서 행렬을 전혀 모른다는 가정하에서 준비를 했다.

행렬이라는 개념은 기본적으로는 표를 간략화한 것이라고 보면 될 것 같다. 행렬의 (i,j)성분을 각각 행과 열로 대응시켜서 위의 그림처럼 정의를 하며, 특수하게 행과 열의 수가 같은 크기의 행렬은 정사각행렬이라고 정의를 하게 된다.
이번 글에서는 행렬의 기본 연산, 행렬에서의 등호, 덧셈, 상수배, 행렬곱 그리고 지수배에 대해서 배울 예정이며, 추가적으로 transpose(전치행렬), inverse(역행렬)에 대해서까지 다룰 예정이다.
먼저, 행렬 A와 B가 같다는 것이 어떤 것인지 정의를 해보자.

예상하는 바와 같이 두 행렬이 크기가 같고, 모든 성분이 같으면 두 행렬이 같다고 정의가 되어 있다.
다음으로, 행렬의 덧셈과 뺄셈이다.

이 부분 역시 위에서 보이는 것 처럼 직관적으로 생각할 수 있는대로다. 같은 크기의 행렬에 대해서 각 성분들을 더하거나 빼주는 것으로 정의가 된다.
예제로 주어진 행렬 A와 B의 합과 차를 보면 쉽게 이해할 수 있을 것이다.
다음은 행렬의 상수배이다.

여기까지는 역시 생각하는대로이다. 모든 성분에 대해 상수배를 해준 결과로 정의를 해준다. 예제를 보면, 두번째 문제의 경우는 위에서 정의한 행렬의 차를 다시 상수배를 통해 확인할 수 있다는 것 역시 볼 수 있다.
다음은 지금까지 정의된 행렬의 연산을 통한 몇 가지 성질들이다.
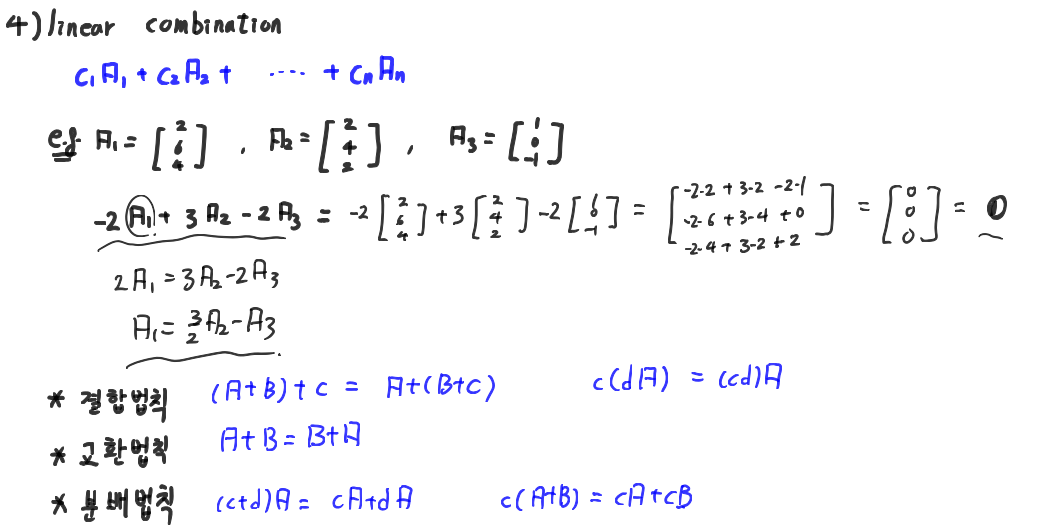
일단은 행렬을 linear combination의 꼴로 나타내줄 수 있으며, 예제에서 보는 바와 같이 우리가 다항 방정식을 정리하는 것 처럼 변수에 대해 행렬에 대한 식을 정리해 줄 수 있게 된다.
그리고 행렬의 덧셈과 상수배에 대해서는 결합법칙, 교환법칙, 분배법칙이 모두 성립한다는 것 역시 확인을 해줄 수 있다.
다음으로는 이제 조금 우리가 생각하는바와 다른 부분인데, 행렬의 곱에 대한 부분이다.

먼저, 일반적인 행렬의 곱을 보기 전에, Row Column Product를 먼저 정의해보면, 위의 그림과 같이 정의를 해줄 수 있다. 이 부분은 우리가 두 벡터의 내적을 계산해줄 때 쓰던 방법과 유사하기 때문에 어렵지 않게 받아들일 수 있을 것 같다.
그리고 그걸 확장시켜서 두 행렬의 곱을 정의하게 된다. 일단 그림에서 보이는 바와 같이 행렬 A와 B의 곱 AB가 정의가 되기 위해서는 A행렬의 열의 크기와 B행렬의 행의 크기가 같아야 정의가 되며, 그 결과는 행렬의 (i, j) 성분을 보면 Row Column Product의 결과와 같다는 것을 볼 수 있다. 즉, 행렬의 곱은 Row Column Product의 결과를 다시 행렬로 모두 모아서 저장해준 것이라고 보면 될 것 같다.

예제를 통해 확인을 해볼 수 있다. 어렵지 않게 따라갈 수 있을 것이다. 특히, 2번 문제를 보면 곱의 결과가 원래의 행렬과 같은 행렬이 나오는 것을 알 수 있다. 앞의 2X2행렬은 행렬곱의 항등원이 되며, 이는 identity matrix(단위행렬)이라고 정의가 된다. 일반적으로 nxn 크기에 대해서 단위행렬은 대각성분만 1이고 나머지 모든 성분은 0인 행렬로 정의가 된다.
다음은 행렬곱에 대한 몇 가지 성질들이다.
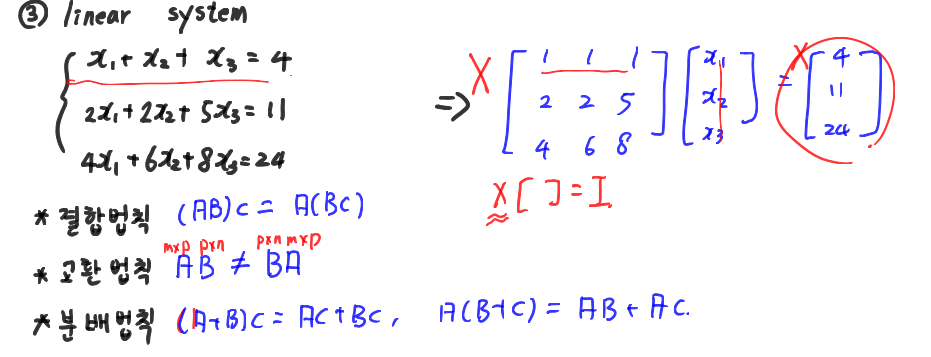
일단, linear system을 보자. 한국말로하면 연립방정식인데, 연립방정식을 오른쪽과 같이 행렬의 곱의 형태로 나타내줄 수 있다. 그리고 이렇게 나타낸다고 하면, 적절한 행렬 X를 양번에 앞에 곱해주면 왠지 x를 쉽게 구해줄 수 있을 것 같은 느낌이다. 이에 대해서는 뒤에서 다시 이야기하도록 하자.
마찬가지로 행렬의 곱에 대해서도 결합법칙과 분배법칙은 성립한다. 하지만, 일반적으로 교환법칙은 성립하지 않는다. 간단하게 mxp 행렬 A와 pxn 행렬 B를 생각하면 BA는 정의도 되지 않는다는 것을 확인할 수 있으며, 정사각행렬들의 곱에 대해서도 일반적으로 교환법칙은 성립하지 않는다.
다음은 행렬의 기본연산들 중에 마지막인 지수승에 대한 정의이다.
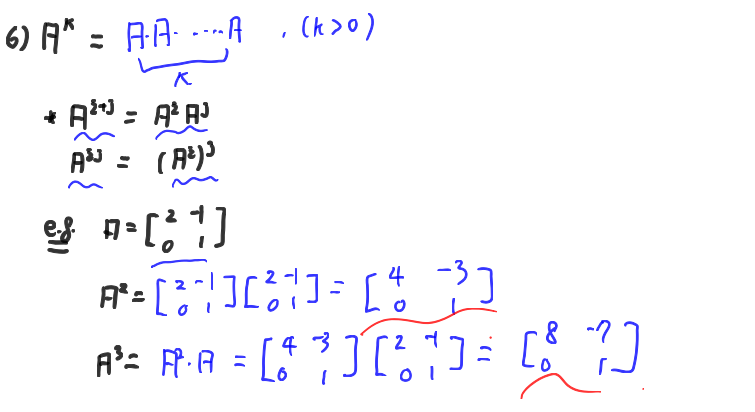
마찬가지로, 일반적인 유리수에 대한 지수승과 똑같이 정의되지만, 그 곱이 행렬곱으로 정의가 되게 된다.
이제 조금 더 나아가서 행렬에 대해서 새로운 개념들을 정의해보고자 한다.
첫번째는 transpose이다.

Transpose는 기본적으로, 같은 정보를 포함하고 있지만 다른 형태의 행렬을 만들어주는 작업이다. 그 방법은 행렬의 행과 열을 바꿔주는 것으로 정의가 된다. 특수하게 complex number(복소수)의 경우에서는 conjugate transpose가 켤레복소수의 전치행렬로 정의가 된다.
예제를 통해 전치행렬의 개념을 한 번 더 확인해볼 수 있으며, complex number에 대해서는 transpose와 conjugate transpose가 다르게 나오게 되는 것 역시 확인을 해줄 수 있다.
자연스럽게 이런 의문이 들 수 있다.
"그래서 전치행렬을 어디에 쓰는건데?"
사실 우리는 알게 모르게 이 개념을 써오고 있었다.

벡터의 내적이다. 우리는 벡터의 내적을 정의하고 그 계산은 두 벡터의 성분을 모두 알 때 각 성분들의 곱의 합으로 구한다고 배웠다. 이 벡터를 nx1의 행렬로 표현해보면, 벡터 a와 b의 내적은 사실 (a^T)*b로 행렬을 전치행렬 시킨 것과의 곱으로 표현이 된다. 이렇게 행렬의 곱의 차원을 맞춰주기 위해서 전치행렬은 많이 사용이 된다.

마찬가지로 transpose의 operation들을 위의 그림과 같이 정의를 할 수 있다. 이 중 특이한 부분은 두번째가 될 것 같은데, 이에 대해서 간단하게 증명을 해봤다.
(AB)^T의 (i, j) 성분은 transpose의 정의에 의해 AB의 (j, i)성분과 같게 되고, 그것을 표현하면 위와 같다. 그리고 우변의 (B^T)(A^T)의 (i, j)성분은 B^T의 i행과 A^T의 j열의 row column product가 되며, 이는 전치행렬의 정의에 의해 B의 i열과 A의 j행의 곱으로 표현이 되고, 이를 풀어서 써보면, 위의 결과와 같은 결과가 나온다는 것을 확인할 수 있다.
다음으로는 행렬의 symmetric에 대한 정의다.

이 부분은 크게 설명이 필요 없을 것 같다.
마지막으로, 행렬의 Inverse에 대한 부분이다.
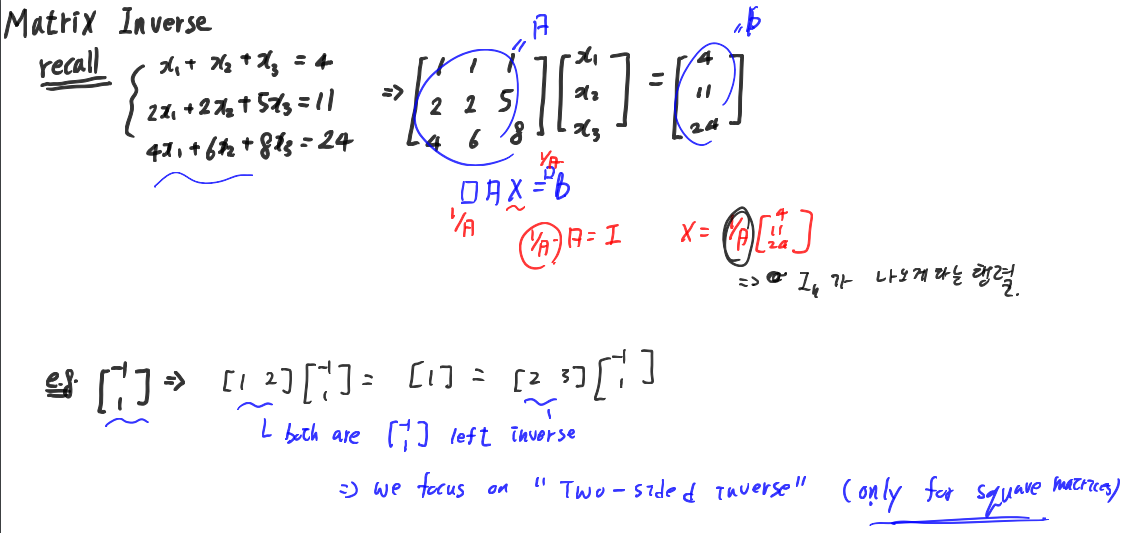
먼저 앞에서 한 부분을 다시 생각해보자. 우리는 linear system을 행렬의 곱 형태로 표현을 해줬다. 위의 그림에서 개념상으로 1/A의 역할을 하는 행렬을 구해줄 수 있다면 우린 x를 쉽게 구해줄 수 있을 것이다. 이 아이디어에서 1/A를 A의 inverse로 정의를 해주게 되며, 이는 A와 곱하여 단위행렬이 나오게 하는 행렬로 정의가 된다.
하지만, 위의 예를 보면, 교환법칙이 성립하지 않는 행렬의 특성을 고려하여, 하나의 행렬에 대해 한쪽 측면에 대한 inverse는 하나로 정의가 되지 않을 수도 있다. 이때문에 우리는 일반적으로 "Two-sided inverse"에 대해서만 관심을 가질 것이고, 자연스럽게 정사각행렬에 대해서만 다루게 된다.

행렬이 invertible하다는 것은 위와 같이 정의가 된다.

예제를 통해 확인해보면, A가 B의 역행렬이라는 것을 AB와 BA가 모두 단위행렬이 나온다는 것을 통해 보일 수 있다.
다음 예제는 A행렬이 invertible하지 않음을 보이는 것인데, 우린 inverse를 구하는 방법을 배우지 않았다. 하지만, 다시 linear system을 행렬곱으로 표현할 수 있다는 사실을 생각해보면, 위와 같이 연립방정식이 유일한 해를 가지면 A가 invertible하다는 것을 보일 수 있다. 하지만, 이 경우에는 어떤 경우에도 연립방정식이 부정해를 갖거나 불능이 되어서 A는 invertible하지 않다는 것을 확인할 수 있다.

다음은 inverse에 대한 몇가지 법칙들이다. 쭉 읽어보면 될 것 같고, 이를 모두 다 증명해보고 넘어가기에는 너무 많기 때문에 uniqueness에 대해서만 확인을 해보면, 가정에서 inverse가 2개가 있다고 가정을 해도 결국 그 두 행렬은 같다는 결론이 나온다는 것을 확인할 수 있다.

negative matrix power 역시 inverse를 통해 정의가 되며, 예제를 보면, A에 대한 항등식을 이용해서 A의 역행렬을 구하는 것 역시 가능하다는 것을 확인할 수 있다.
이제 드는 의문은 아마 "그래서 그 역행렬을 어떻게 구하는가?" 일 것 이다.
일단 2x2행렬에 대해서 살펴보자.

2x2행렬에 대해서는 위와 같이 공식처럼 정의가 되는 것을 확인할 수 있다.
그렇다면 3x3, nxn 행렬은 어떻게 구할까?
사실 이 부분은 2x2 행렬처럼 쉽게 정의가 되지는 않는다. 이에 대해서는 선형대수학을 통해 자세히 배우게 된다.
마지막으로 행렬 기반의 프로그래밍 언어인 Matlab을 통해 행렬의 기본 개념들을 실습을 해보고자 한다.
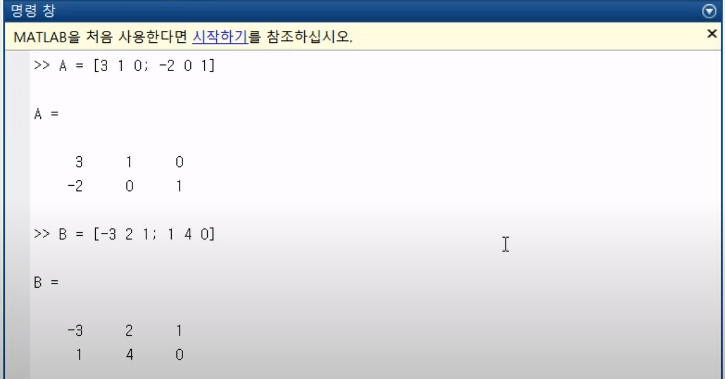
행렬은 일단 대괄호에 행 바꿈을 ;으로 해서 정의를 해줄 수 있다.
기본 연산들에 대한 것은 생략하고, 명령어가 필요하거나 추가 설명이 필요한 부분만 언급을 하도록 하겠다.

N = [2 -1; 0 1]로 정의가 되어있다.
매트랩에서는 곱하기 연산을 기본적으로 행렬곱으로 정의를 해주고 있다. 하지만, 때에 따라서 우리는 각 행렬의 성분들을 곱한 결과를 구해주고 싶을 수도 있다. 이 경우에는 연산자 앞에 .을 붙여서 해주면 행렬들의 성분끼리만 계산을 해준 결과가 나온다.

전치행렬의 경우는 A라는 행렬에 대해서 A.' 또는 transpose(A)로 구해줄 수 있다.
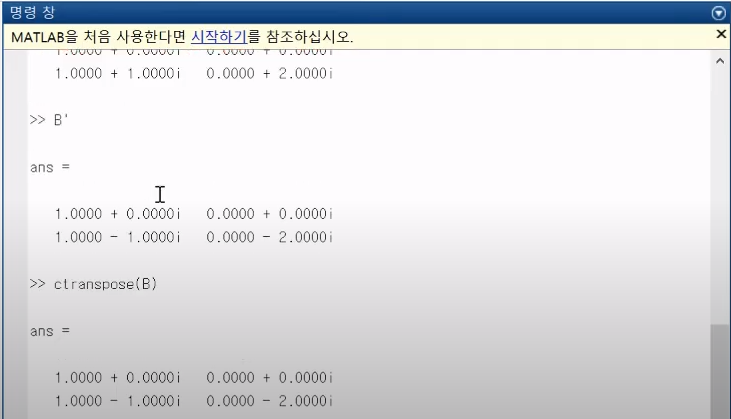
B = [1 1+i; 0 2i]로 정의가 되어있다.
conjugate transpose의 경우는 행렬 B에 대해서 B' 또는 ctranspose(B)로 구해줄 수 있다.

A_1 = [2 -1; -1 1]로 정의가 되어 있다.
역행렬의 경우는 A_1에 대해서 inv(A_1)로 구해줄 수 있으며,
inv(A_1) == B_1의 명령어는 매트랩에게 A_1의 역행렬이 B_1과 같냐고 물어보는 것이다. B_1은 이전에 A_1의 역행렬과 같은 행렬로 정의를 해놓았으며, 이 결과의 출력은 bool로 나타나게 된다. 컴퓨터에서 1은 True, 0은 False를 나타내기 때문에 결과로 모두 1이 나오며, 이는 모든 성분이 같다는 것을 의미하게 된다.
이렇게 행렬의 기본에 대한 설명과 이를 matlab으로 실행하는 것으로 마무리를 한다.
<추가된 내용>
이 수업들을 원격으로 해서 내 유튜브 계정에 수업 영상들이 남아있었는데, 혹시나 해서 일부공개는 그대로 넣어놓고 재생목록을 만들어두었으니 도움이 될지는 모르겠지만 관심 있으면 아래에서 영상도 확인할 수 있습니다.
https://youtube.com/playlist?list=PLT8Ck3FhPFERRvX1Y1_Ukq97u6z6pkyCG
'전공 공부' 카테고리의 다른 글
| (알아두면 좋은 정보) 구글 스칼라 알림 설정하기 (0) | 2020.11.18 |
|---|---|
| Laplace Transform Matlab으로 해보기 (0) | 2020.05.12 |
| 수치적 적분: 적분의 근사 방법 (0) | 2020.04.07 |
| 다양한 적분 방법 : 삼각치환법과 부분 분수를 이용한 적분 (0) | 2020.03.31 |
| 함수의 극한 정의 : 입실론-델타 논법 (4) | 2020.03.24 |




