| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 드림라이브존
- 프로야구
- V1구역
- 제주도
- 리클라이너석
- 원정
- 5G
- 오스너예가다이얼
- 티스토리챌린지
- 텐동텐야
- 창원nc파크
- 술담화
- 일엽편주
- SK 와이번스
- network slicing
- 신해바라기 분식
- 제주 담스테이
- 전복 김밥
- 직관
- 제주도 자전거여행
- LG TECH CONFERENCE 2023
- 아이오닉5
- 오블완
- sk와이번스
- 후기이벤트참여
- 담화탁주
- 올스타전
- 롯데시네마 현풍
- 원정응원단석
- 환상자전거길
- Today
- Total
개루프이득의 블로그
함수의 극한 정의 : 입실론-델타 논법 본문
생각지도 못한 학부 수학과목의 조교를 하게 되면서 기억 속 저편에 있던, 아니 이미 저장공간 부족으로 삭제되었던 내용들을 다시 복습을 하며 공부를 하고 있다.
이번에는 미적분학 및 미분방정식 수업에서 가장 기초가 되는 함수의 극한에 대해서 복습을 했다.
사실 학부 때도, 입실론-델타논법을 어려워했고 잘 이해를 못 했었다. 그냥 입실론이 주어지면 그에 따라 델타도 주어지면서 점점 줄여나가면서 함수의 극한을 정의한다는 것 정도만 알고 있었고, 직접 연습문제나 예제를 풀어보면서 증명을 하려고 하면 번번히 막혔었다.
그래도 이번에 조교를 하면서 이 부분을 다시 공부하고, 원격강의를 위해 악필이지만 직접 정리를 한 내용이 있어서 블로그에도 되도록이면 쉽게 잘 풀어서 정리를 하고자 한다.
1. 입실론-델타 논법 소개
우리는 적어도 고등교육과정의 수학에서까지는 극한이라는 것을 어느 한점으로 한없이 가까워져 갈 때 수렴하는 값이라는 추상적인 개념으로 배웠고, 이를 그대로 받아들여왔다. 하지만, 수학에서는 이러한 표현을 굉장히 싫어한다. 특히 해석학과 같은 학문에서는 우리가 당연하다고 받아들였던 모든 개념을 수학적으로 엄밀하게 증명을 하기를 원한다. 입실론-델타논법 역시 추상적인 극한의 정의를 엄밀하게 정의를 하기 위한 방법이다.

극한을 어떻게 수학적으로 정의를 할 수 있을까?
위의 그림의 그래프를 한 번 봐보자. 우리는 x가 c에 가까워질 때의 극한값을 알고 싶다. 즉, 일단은 c에서의 x값은 중요하지 않다. 이 때, c를 중심으로 해서 양 방향으로 델타의 크기의 구간을 잡아주어서, 이 구간에 있는 모든 x에 대해, 함수값이 극한값 L에 대해 일정한 오차범위 안에 모두 들어간다고 하면, 그 오차를 계속해서 무한히 줄여나가도, 델타라는 구간의 크기가 정의가 된다면, 그 함수의 c에서의 극한값을 L이라고 정의 할 수 있을 것이다.
즉, 수학적으로는 만들 수 있는 모든 오차한계 입실론에 대하여 f(x)를 L의 오차한계 안에 두기 위해 x와 c사이의 충분히 가까운 거리 델타를 입실론의 함수로 구하거나 계산할 수 있음을 증명하면, 극한값을 정의할 수 있게 된다.
이 아이디어에서 나온 것이 입실론-델타 논법이 된다. 그 정의는 위의 그림의 빨간 네모박스 부분이 된다.
"임의의 입실론에 대하여, 0보다 큰 델타가 존재하며, 그 델타는 c를 중심으로한 델타라는 크기의 구간 안의 x에 대해 x의 함수값이 극한값 L에 대해 입실론이라는 오차한계 안에 존재한다."
즉, 이 정의에서는 증명을 하기 위해서는 델타를 입실론에 대한 함수로 표현할 수 있으면 되며, 그 델타가 꼭 유일하게 구해지지는 않을 수도 있다.
2. 간단한 예제 풀이
이제 입실론-델타 논법을 직접 써보기 위해 간단한 예제문제들을 풀어보도록 하자.
첫번째는 우리가 흔히 아는 1차함수 꼴이다.
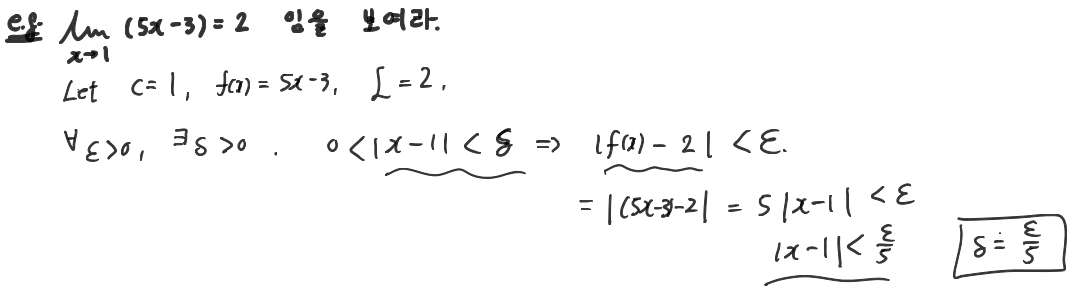
우리는 이 함수가 연속이고, 극한값이 존재한다는 것을 직관적으로 알지만, 이를 배운 입실론-델타논법으로 한 번 증명을 해보도록 하자.
정의를 그대로 사용하기 위해, 각각 c와 f(x), L을 정의를 해주고, f(x)-L 부분을 풀어서 써주면, x-c의 꼴로 풀리게 되어, 델타가 입실론/5로 표현이 되어, 모든 입실론에 대해 델타가 존재함을 쉽게 보일 수 있다.
다음은 불연속 함수에 대한 증명이다.

우리는 역시 이 함수가 우극한과 좌극한이 직관적으로 같아서 극한값이 존재함을 알고 있다.
이를 증명하기 위해서, 극한의 정의에서 c에서의 함수값은 중요하지 않기 때문에, 먼저 x는 2가 아닌 함수에 대해서 봐준다. 그러면, x의 범위가 입실론에 대해서 나타나지게 되는데, 이는 극한값 4에 대해 위 아래로 입실론 만큼의 오차 안에 함수값이 존재하기 위해서는 그 구간 안에 x값이 존재하면 된다는 의미이다.
즉, 2를 중심으로 하는 (2-델타, 2+델타)의 구간이 위에서 구해준 x의 구간 안에 들어가면 되므로, 델타는 위와 같이 두 거리 사이의 최소값으로 정해질 수 있으며, 입실론이 4보다 큰 경우도 같은 방식으로 구해줄 수 있어서, 이 경우 역시 모든 입실론에 대해 델타가 입실론에 대한 함수로 표현할 수 있기 때문에 극한값이 존재함을 보일 수 있다.
3. 극한의 덧셈정리 증명
다음으로는, 입실론-델타 논법을 통해 극한의 정리를 증명해보도록 할 것이다. 가장 간단하게 덧셈정리를 증명해보도록 하자.
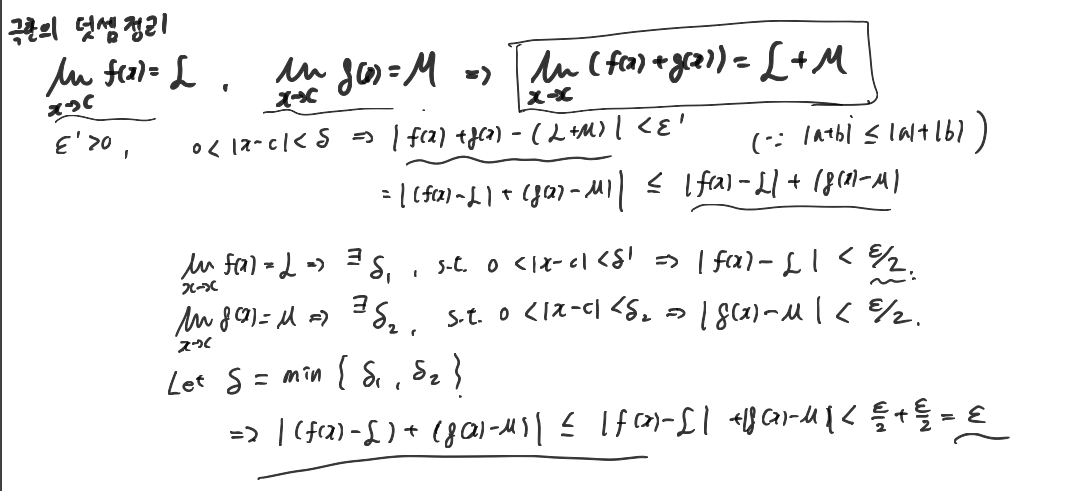
아마 어렵지 않게 이해할 수 있을 것 같다. 가정으로 사용해준 정의를 그대로 이용하여 덧셈에 대한 극한을 삼각부등식으로 풀어주어 정의를 해준다. 약간 꼼수라고 하면, 어차피 모든 입실론에 대해 델타가 정의가 되기 때문에, 가정에서의 정의를 증명의 편의를 위해 입실론/2로 표현을 해 주었다.
4. 연습문제 풀이
마지막으로 두 문제 정도 연습문제를 풀고 마무리를 하고자 한다.
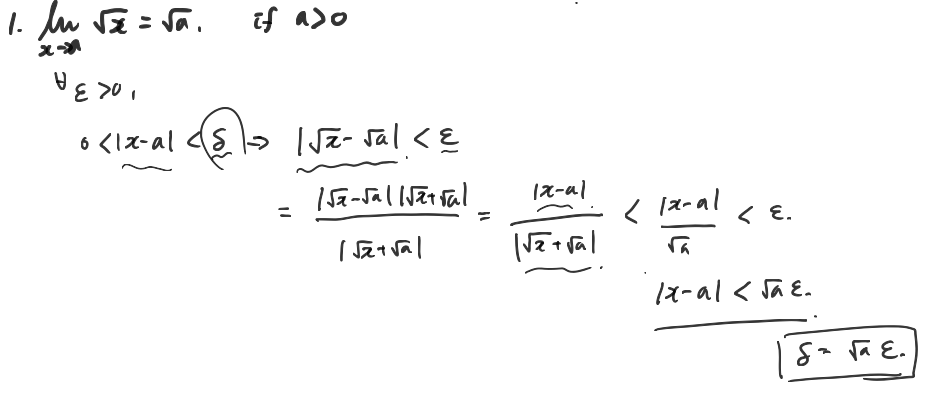
입실론-델타 논법을 이해했다면 어느 정도 눈치를 챘겠지만, 결국 입실론에 대한 부등식을 잘 바꿔줘서 델타에 대한 꼴로 나타내주는 것이 전부이다. 이 문제의 경우는 그냥 보기에는 잘 안 보이지만, 분자, 분모에 같은 값을 곱해주어서 합차공식으로 원하는 꼴로 표현을 해줄 수 있는 경우이다.

마지막으로는, 내가 보기에는 약간 꼼수 같은데, 어차피 델타가 유일하게 정의가 되는 것이 아니기 때문에 입실론이 큰 경우 일반적인 기준값으로 델타를 정해주고, 거기서 국소값에 대한 델타를 표현해주는 방법이다 이 경우는 일단 델타가 1일 때로 지정을 해주고, x의 범위를 통해 작은 입실론 값에 대해서 델타를 표현해주어 그 델타를 입실론에 대한 함수와 1 중 최소값으로 표현을 해주게 한다.
사실 입실론-델타 논법이 쉬운 내용은 아니고, 아직 나도 완벽하게 이해가 된 것 같지는 않다. 수학적으로 깊게 들어가면 이렇게 모든 것을 수학적으로 증명을 하고자 한다는 특징이 있는 것 같다. (그게 내가 해석학 수업을 드랍한 이유이기도 하고....)
나도 완벽하게 이해를 하지는 못했지만, 적어도 지금 이해한 만큼은 잊어버리지 않도록 이렇게 기록을 남겨놓고자 한다.
<추가된 내용>
이 수업들을 원격으로 해서 내 유튜브 계정에 수업 영상들이 남아있었는데, 혹시나 해서 일부공개는 그대로 넣어놓고 재생목록을 만들어두었으니 도움이 될지는 모르겠지만 관심 있으면 아래에서 영상도 확인할 수 있습니다.
https://youtube.com/playlist?list=PLT8Ck3FhPFERRvX1Y1_Ukq97u6z6pkyCG
'전공 공부' 카테고리의 다른 글
| 수치적 적분: 적분의 근사 방법 (0) | 2020.04.07 |
|---|---|
| 다양한 적분 방법 : 삼각치환법과 부분 분수를 이용한 적분 (0) | 2020.03.31 |
| Delay jitter란 무엇이고, 왜 필요할까 (2) | 2019.11.14 |
| Edge Computing이란? (0) | 2019.08.25 |
| SDN과 NFV의 차이 (0) | 2019.08.19 |




